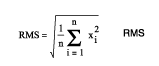雜訊可定義為電子系統想屏除的訊號,亦即使音訊品質下降或精準測量出現誤差的原兇。電路板與系統層級的電路設計工程師亟欲判別設計時可能遇到的最大雜訊、降低雜訊的方法以及精確驗證其電路設計的測量技術。
固有雜訊(Intrinsic noise)與外來雜訊(extrinsic noise)是影響電路的兩種基本雜訊。外來雜訊是由外界產生,數位切換、60Hz雜訊和電源供應切換都是常見的外來雜訊。固有雜訊是由電路元件本身產生,寬頻雜訊、熱雜訊和閃爍雜訊(flicker noise)則是最常見的固有雜訊。此系列文章將說明如何透過計算和SPICE模擬預測電路的固有雜訊強度,同時討論雜訊測量技術。
熱雜訊
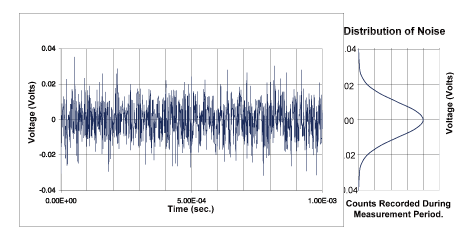
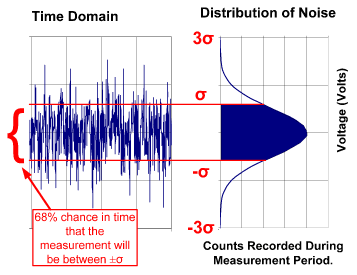
熱雜訊是由電子在導體內的隨機移動產生。由於這種移動會隨著溫度而增加,熱雜訊振幅也會隨著溫度而變大。熱雜訊可視為零件(例如電阻)兩端電壓的隨機變動。(圖一)是熱雜訊在時域的形狀(標準示波器測量),若以統計方式觀察此隨機訊號,會發現訊號能以高斯分佈(Gaussian distribution)來表現。(圖一)右側的高斯分佈圖顯示隨機訊號與時域訊號的關係。
熱雜訊的功率與溫度和頻寬成正比,此正比關係能以一個簡單的功率公式以電壓和電阻來表現,請參考(公式一)。此公式可估計電路的均方根(RMS)雜訊值,並可說明在低雜訊電路中,使用低阻抗元件的重要性。
公式一能計算出均方根雜訊電壓。工程師常想知道「最壞情形下的雜訊為何?」換言之,峰對峰電壓工程師最感興趣的議題。將均方根熱雜訊電壓轉換為峰對峰雜訊時,熱雜訊即對應於高斯分佈。有些以統計關係為基礎的簡單經驗規則可用來將均方根值轉換為峰對峰值,但本文在介紹這些規則之前將先討論一些數學背景。本文的重點是複習這些統計學的背景資料,接下來的文章則會涵蓋實際類比電路的測量與分析。
機率密度函數
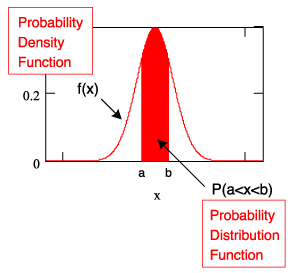
構成常態分佈函數的數學方程式稱為「機率密度函數」,可參考(公式二)。將某段時間測量的雜訊電壓繪成直方圖,即可得到此函數的圖形。(圖二)同時顯示了機率密度函數以及測量所得的雜訊直方圖。
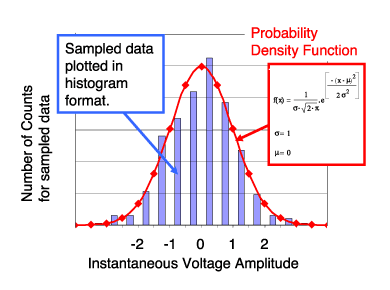
| 《圖二 測量得到的分佈值和重疊其上的機率密度函數》 |
|
機率分佈函數
機率分佈函數(Probability Distribution Function)是機率密度函數的積分。此函數非常有助於判斷一個事件在某段時間的發生機率,請參考(公式三)和(圖三)。舉例來說,假設(圖四)是雜訊機率分佈函數,此函數意義為在任何時間測量到-1V和+1V之間(亦即 (-1, 1)區間)雜訊電壓的機率是30%。