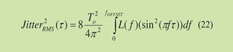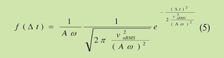|
|
| 隨機雜訊對時脈抖動影響的理論與實驗 |
|
【作者: Ken Yang,Steve Lee】 2005年09月05日 星期一
|
|
瀏覽人次:【12135】
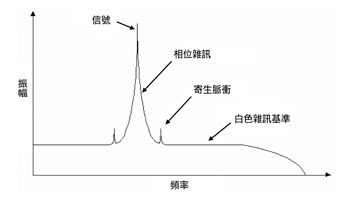
時脈抖動(Timing Jitter)與雜訊可以說是工程應用上最不被了解的概念之一,但卻也是數位與類比設計中最關鍵參數的一環,特別是在高速通訊系統中,不良的抖動情況會造成較高的位元錯誤率並限制系統的傳輸速度。時脈抖動通常定義為數位信號短時間內偏離期理想位置的大幅變化,造成隨機時脈抖動的原因有幾個,包括寬頻雜訊、相位雜訊、寄生脈衝(spurs)、電壓變化率(slew rate)以及頻寬等,其中相位與寬頻雜訊為隨機,而寄生脈衝則是由各種可確認干擾信號,如相互干擾(crosstalk)與電源耦合所造成的固定響應,而在以下的文章中可以看出,電壓變化率與頻寬同時也會對時脈抖動帶來影響。(圖一)描述了包含三個雜訊源的非理想正弦波波形,(圖二)則是一個隨著時間累積抖動信號的數位信號波形。
這篇文章的目的主要是解釋並展示時脈抖動與這三個雜訊源的直接關聯性。
寬頻雜訊對時脈抖動的影響
正弦波中時脈抖動
所有的電子元件,特別是放大器與邏輯元件都會產生寬頻雜訊,又稱為雜訊基準(noise floor),寬頻雜訊是散粒雜訊(shot noise)與熱雜訊(thermal noise)的組合,常見於二極體與電晶體上,散粒雜訊是由半導體內接面上電荷隨機跳越電位屏障引起,另一方面,熱雜訊則不會受電流流動影響,而是主要由載子的隨機熱移動所造成,例如在MOSFET的閘極與通道阻抗,熱雜訊功率大小與阻抗及溫度成正比。
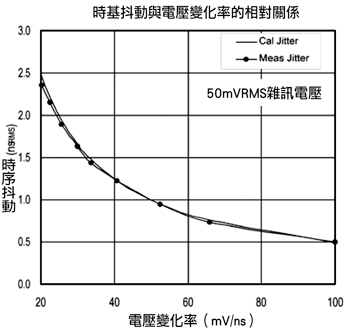
寬頻雜訊對時脈抖動的影響在目前元件的運作頻寬已經進入數GHz的趨勢下已經變得相當重要,舉例來說,具備40GHz頻寬、10dB雜訊指數(noise figure)、20dB小信號增益與0dBm輸出功率的寬頻放大驅動電路會產生-38dBm的雜訊輸出(-174dBm + 10dB + 20dB + 10log10(40GHz)),因此訊噪比(Signal-to-Noise Ratio;SNR)為38dB,在這樣的SNR等級下,寬頻雜訊在時脈抖動的影響上就佔了相當大的部分,整體均方根(Root-Mean_Square;RMS)雜訊電壓為整體頻寬內雜訊基準的累積,(圖三)顯示RMS雜訊如何轉換成時脈抖動。
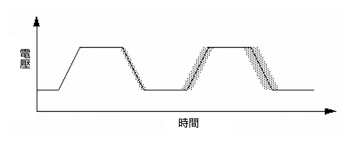
| 《圖二 這個時脈信號中的隨機雜訊與寄生脈衝會造成時基抖動,並隨時間累積》 |
|
以數學上來說,可以用以下的方程式來表示內含寬頻白色雜訊的正弦波:
其中A為振幅,為角頻率,則為時間t時的雜訊電壓。隨機雜訊擁有高斯(正規)分佈特性,這個雜訊電壓的概率分佈函數為:
其中為RMS雜訊電壓。要了解雜訊電壓如何轉換成時脈抖動,將送到時脈抖動測量儀器,例如擁有直方圖(histogram)功能的取樣示波器的輸入端,每一次與通過0V臨界電壓時,直方圖上就增加一個資料點。如圖三中,在時間時,雜訊信號可能會達到臨界點,因此會在取樣點的前或後時間讓時脈抖動加入到直方圖上。可以將方程式二設為來計算時脈抖動的概率密度函數,得到直方圖中的時脈抖動分佈函數。
方程式三可以透過假設與正弦波週期時間比較時較小,因此來加以簡化:
|
因此方程式三就變成方程式四:
將方程式四中各分子與分母除上,可以得到:
方程式五是一個與方程式二中高斯(Gaussian)分佈類似的時基抖動分佈函數,只有的倍率差別,因此RMS時基抖動就成為:
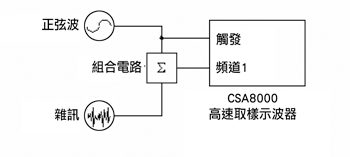
| 《圖四 時基抖動測試安排#1:將雜訊加到純淨正弦波上》 |
|
|
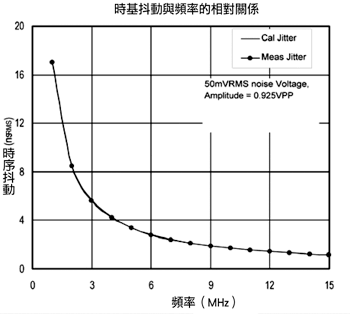
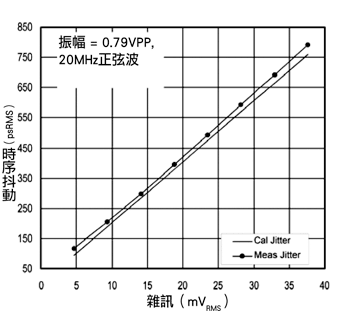
(圖四)中的測試安排主要用來驗證方程式六,使用純淨的正弦波加上寬頻雜訊組合後送到測量零交越電壓的取樣示波器,為了確保得到有效的結果,輸入寬頻雜訊必須要比示波器的雜訊基準還高,(圖五)與(圖六)分別顯示實驗的結果,圖五顯示了抖動信號作為固定RMF雜訊輸入頻率的函數,圖六則顯示具備固定頻率的RMF雜訊電壓函數,經由測量以及計算所得抖動曲線間的相似性證明了方程式六可以用來將寬頻雜訊轉換成為時基抖動信號。
常見波形中的時基抖動
經過簡單的修改,方程式六同時也可以應用在其他波形的時基抖動轉換上,在定義上,方程式六中的為0V臨界點的電壓變化率S,任何已知臨界點電壓變化率的波形都可以用來將轉換為,原因是,如圖三所示,代入方程式二後可以得到方程式七:
將方程式七中的分子與分母除以S可以得到:
方程式八與方程式二中的高斯分佈類似,只有1/S倍率差別,因此RMS時脈抖動信號就成為:
圖四中的測試安排同樣地可以用來驗證方程式九,只是將正弦波以可調電壓變化率的方波取代,時脈抖動則在方波上升緣的50%處測量,(圖七)中的結果驗證了方程式九的計算結果。
圖七中的資訊帶來了一個值得注意的現象,那就是具有較快電壓變化率的波形時脈抖動較小,但要得到較快的電壓變化率則需要較大的工作頻寬,造成系統RMS雜訊的提升,原因是RMS雜訊與頻寬成正比,在了解了這個關係以後,系統設計工程師必須謹慎地選擇電壓變化率與頻寬以便將時基抖動降到最低。
相位雜訊對時基抖動的影響
相位雜訊出現在所有的主動與阻抗式元件上,在振盪器上特別嚴重,這些振盪器包含自由運轉的石英振盪器與時脈回復應用上的鎖相振盪器,相位雜訊是一個表示頻譜純淨度的規格,例如,振盪器的輸出在頻域中理想上是一個以垂直線出現的單一頻率純淨正弦波,但是在現實上,振盪器中卻有幾個雜訊源會造成輸出頻率偏離原本理想的位置,因此產生接近接近載波,也就是基本頻率的裙帶(skirt)頻率,如(圖八)所示,通常稱為相位雜訊,這些頻率因雜訊源對振盪器進行調變所產生,通常出現在高於雜訊基準並接近載波頻率處,相位雜訊通常定義為1Hz單位處載波偏移頻率的雜訊功率與載波功率的比值,由於雜訊源頻率會對信號進行調變而產生相位雜訊,因此相位雜訊不受電壓變化率的影響。
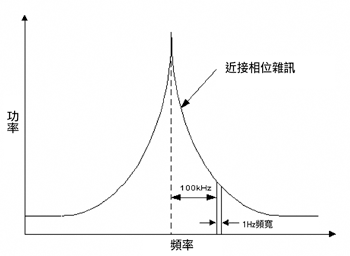
| 《圖八 輸出頻譜上的群帶(skirt)頻率由雜訊頻率對振盪器進行調變而產生》 |
|
由於大部分時脈抖動量測設備的限制,通常在頻域中測量相位雜訊要比在時域中測量時脈抖動更容易決定低雜訊信號的純淨度,例如大部分的時脈抖動量測示波器只能測量到最低1ps的RMS信號,而大部分常見的即時示波器則只有7GHz的最高頻寬,但在另一方面,相位雜訊設備則可以測量最佳低雜訊振盪器的雜訊等級,要比時域中的1ps低得多,同時可以提供高達40GHz的頻寬。
相位雜訊與時脈抖動間的轉換在之前已經被討論過[1-2],要得出相位雜訊與時脈抖動間的相關方程式,先考慮方程式十為包含相位雜訊的正弦波:
其中A為振幅,fo為額定頻率(nominal frequency),為相位雜訊。時脈抖動通常是在兩個或更多個週期範圍的0V交越點測量,在0V交越時,方程式十中括號內的數值為2N:
|
其中t1為第一個零交越點,t2為第N個零交越點,代入這兩個方程式可以得到:
兩個零交越點間的時間為週期數加上時脈抖動:
其中To T為週期或1/fO,為N個週期後所累積的時基抖動,將方程式十四代入方程式十三可以得出:
重新整理方程式十五並去掉2N可以得到方程式十六的時脈抖動:
因此平方RMS時脈抖動為:
由於是一個固定程序,因此
其中為的頻譜密度,f則為偏移(傅立葉)頻率,因此方程式十七中的中間部分就成為:
其中為的自相關函數,而則等於N個週期後時間,N個週期後時間的平方RMS時基抖動為:
利用代數等式並假設相位雜訊接近載波而且對稱,也就是說由-fOFFSET 到0的累積值會等於0到+fOFFSET,那麼方程式二十可以寫成:
大約等於近接(cloase-in)相位雜訊[3]的相位雜訊,也就是說傅立葉偏移頻率要比載波頻率低上許多:
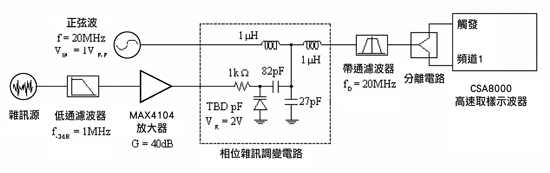
| 《圖九 測試安排#2:利用相位調變產生相位雜訊與時基抖動》 |
|
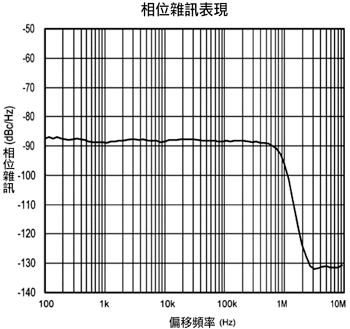
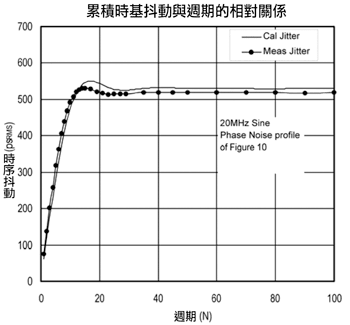
在(圖九)中的測試安排應用了相位調變電路[4]以便驗證方程式二十二,相位調變電路提供一個產生無寄生雜訊的可變相位雜訊源的方法,電路的輸出首先透過取樣示波器測量時脈抖動,接著再用頻譜分析儀(沒有顯示在圖中)來測量相位雜訊,(圖十)為這個電路的相位雜訊表現,與鎖相振盪器的雜訊類似,相位雜訊在迴路頻寬內固定,在頻寬外則衰減,使用數值積分來對方程式二十二進行積分,可以得到(圖十一)中的特定週期時脈抖動累積結果,圖十一中的曲線讓方程式二十二得到了驗證。
寄生雜訊對時脈抖動的影響
寄生雜訊(Spurious Noise)也會對時脈抖動造成影響,特別是在振盪器內,寄生雜訊可以由鎖相迴路參考寄生雜訊、電源耦合、與鄰近電路的交互干擾以及信號源產生,如圖一中所示,這些寄生雜訊通常以接近載波頻率的小突波表現,方程式二十二可以用來找出寄生雜訊與時脈抖動的相關性,由於寄生雜訊只會在特定頻率發生,因此方程式二十二中的積分函數可以以加法代替:
同樣地,為N個週期後的時間,由於方程式二十三中並未假設寄生雜訊為對稱,因此將它乘以4而不乘以8,載波兩端的寄生雜訊必須包含在時脈抖動的計算中,L(fn)為相對於載波,也就是目標信號的寄生雜訊振幅大小,通常以dBc為單位,fn則是第N個寄生雜訊的偏移頻率,(圖十二)中顯示了在載波頻率兩端100kHz偏移處振幅為-40dBc寄生雜訊的方程式二十三繪圖結果,透過將電壓控制石英震盪以一個正弦波調變來在載波任一端產生順便雜訊驗證方程式二十三。
整體抖動
如前所述,寬頻雜訊、相位雜訊與寄生雜訊為時脈抖動的主要來源,寬頻雜訊完全隨機同時無相關性,因此產生的時脈抖動無法累積,但後兩者通常會產生累積時脈抖動,因此平方整體時脈抖動為三個平方時脈抖動的總和。
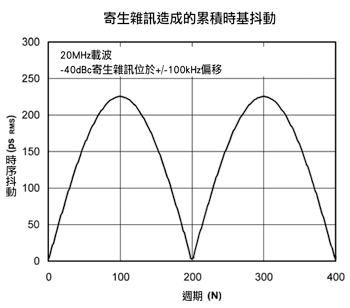
| 《圖十二 在載波頻率兩端100kHz偏移處振幅為-40dBc寄生雜訊的結果》 |
|
結語
實驗與計算結果間的相關性顯示了三個主要雜訊源與時脈抖動兩者間的關係,高速系統的設計工程師可以使用方程式九、二十二與二十三來將雜訊轉換成時脈抖動。(作者任職於Maxim Integrated Product)
|
|
|
|
|
 |
︱ |
Copyright ©1999-2024 遠播資訊股份有限公司版權所有 Powered by O3 v3.20.2048.52.14.104.255 |
地址:台北數位產業園區(digiBlock Taipei) 103台北市大同區承德路三段287-2號A棟204室
電話 (02)2585-5526 #0 轉接至總機 / E-Mail: webmaster@ctimes.com.tw |
|
|