通常我們會發現,為什麼多數商業用的整合型delta-sigma轉換器裝置,對抖動的敏感度很低呢?而delta-sigma轉換器在取樣前,利用濾波器來消除高階超音波量化雜訊中的抖動調變影響。要降低在Delta-Sigma轉換器內抖動的靈敏度,本文要介紹的就是一些相關可用的技術。
切換電容式濾波器
取樣或是重新取樣,是發生在取樣信號及持續時間信號之間的界面,並不是每次都是介於數位與類比間的界面。例如:切換電容式濾波器,它就操作在取樣信號範圍內的類比信號。
在delta-sigma ADC中,超音波量化雜訊是delta-sigma調變器製造出來的產物,如(圖一)所示。如果這類比過濾器在調變器內,被設計成切換電容式濾波器那樣,則雜訊會被持續在取樣信號範圍內。在delta-sigma DAC中,DAC超音波雜訊的輸出,是可以利用切換電容式濾波器來衰減。
Multi-Bit Noise-Shaped轉換器
由於整合切換電容式濾波器必須夠大,才能有好的雜訊性能比。藉由增加在量化器內位元的數目,調變器內的量化雜訊將會進一步降低,所以在相同的比例下,會減少超音波雜訊。例如,ADI(Analog Device)的AD1855,有64階的調變器,而且不需要使用切換電容器的濾波器。
抖動感應的振幅調變
還有一種解決抖動高靈敏度的方法,即利用超音波量化器雜訊的調變。它是感應抖動時間調變與抖動振幅調變方法的合併。
一般而言,DAC通常是電流或是電壓輸出,所以是不受取樣頻率的影響。但是,DAC在每個取樣時,通常是利用電荷充電的方法,所以電流輸出會被取樣頻率分成均等部分。在這情況下,取樣抖動會產生振幅調變的影響,若結合了單純的抖動時間調變後,就成為一個有利解決抖動高敏感度的方法。這類的DAC,取樣抖動所產生的振幅調變影響如(公式一)所示。
振幅調變與單純的抖動調變合併,則會產生,如(公式二)的情形。
這合併後的邊頻帶應該是((i-(j)及((i+(j)的頻率,而不是調變頻率(i,(i在這裡是指超音波(而且這邊頻帶偏移(j是非常大的),所以從公式二可以得知,降低了在任何邊頻帶抖動到音頻頻帶的撞擊(即振幅變小),其頻率落在的範圍,大概的比率,是介於超音波頻帶及音頻頻帶間。
若這信號是屬於在高音量及高頻率(超音波),而且邊頻帶偏移是非常大的(超音波抖動信號),如此一來,邊頻帶可以被調變降到更低的頻率。這技術可以降低抖動調變超音波雜訊,減少它對音頻帶中所帶來的衝擊,例如:超取樣比率大約是256:1。
速率轉換器的取樣抖動
取樣速率轉換器(SRCs)通常使用在轉換信號,從一個取樣速率到另一個取樣速率。這轉換包含著在輸入資料串取樣點間,插入一新的取樣點值。
這兩個取樣速率需有精確的整數關係,這樣新的取樣點才可以在無誤差下被決定。在下面要舉的例子中,它有可能在沒有取樣抖動情況下做轉換,但是輸入與輸出的資料串是需要同步的。例如:一個44.1kHz到96kHz的取樣速率轉換器,可以使用數學關係320/147來達到。輸出串的時間取決於輸入串,所以每147個輸入取樣必須符合320個輸出取樣。這內插法濾波係數可以由這精確關係為基礎來計算,這類的SRC被稱為同步取樣速率轉換器(SSRC)。
取樣速率轉換器經常會有輸出取樣頻率無法鎖住輸入頻率,或者是一些儀器被設計為保留部分靈活性,用來處理任意相關的輸入與輸出時間。在這例子中,這轉換器較為複雜,而且包含了一些演算法,其作用是以它們實際抵達的時間為基礎,用來試著追蹤介於輸入與輸出取樣的關係。這類的SRC被稱為異步取樣速率轉換器(ASRC)。
虛擬時間解析度
演算法利用ASRC從一串取樣時脈的時間,來評估時間關係,並且量測其它較高同步的時脈。這抖動的量測是取決於量測時脈的結果。
例如,在轉換時脈從48kHz到96kHz時,系統時脈工作在256×96kHz。而這40ns的解析度會產生時間量化抖動的振幅,並且會影響時間追蹤演算法的值。
這潛在的取樣抖動來源通常是有一強的頻譜元素:例如48kHz時脈是5ppm,而且256×96kHz速率是6ppm,這樣40ns的量化抖動在大約25Hz(256×96kHz×1ppm)的速率會是鋸齒狀。
虛擬抖動衰減特性
通常ASRC時間估算的演算法會有抖動衰減特性,這可以看成是帶有轉角頻率的低通濾波器。不過,由於這是一個數值處理過程,如果這裝置有足夠的數學解析度,濾波轉角頻率會變成非常低,這意味著ASRC已經有較高的抖動衰減。
由於整合ASRCs已不再昂貴,所以對於DACs取樣抖動的有效排除,被視為低成本的方案。輸出取樣頻率可被固定在低抖動,自由運轉晶體的振盪器,接收的資料串可被轉換為ASRC取樣頻率。在DAC時脈的量測,可能顯露出晶體振盪器的低抖動。
無論如何,在ASRC內的再取樣過程需要被考慮,由於ASRC抖動是由時間演算法,在數字值產生的單純偏差所產生的,它無法直接被計算出來。但是,它可以藉由測試在高頻率、高振幅的數位音調信號通過裝置時的影響來評估結果。
取樣抖動轉移函數
通常要評估ADC、DAC或是ASRC,只要透過抖動的轉移函數,就可以對於裝置的抖動性能,在音頻信號上的影響進行評估。然而,對於ASRC來說,這有可能是唯一的量測方法。
在(圖二)顯示的頻率頻譜,是利用一個12kHz音調在-3dB FS刺激DAC,這個數位輸入信號對DAC來說,是被使用在回復取樣時脈,而且在輸入上,寬頻帶抖動的影響是提升噪音底部均衡的遍及頻帶。
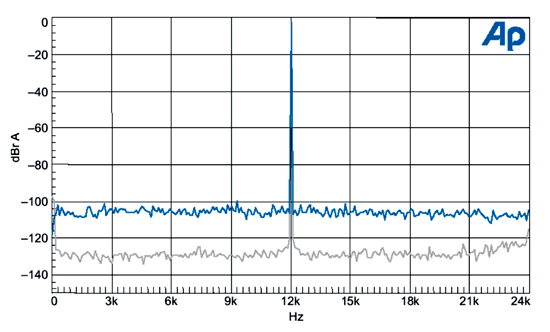
| 《圖二 DAC的FFT,灰色不含寬頻抖動,藍色含9.8ns峰對峰值的寬頻抖動》 |
|
抖動衰減並不是一個平坦的響應,由於抖動刺激是平坦的,所以調變影響也是平坦的,因此在這種情況下沒有抖動衰減。
從分析儀報告指出,在22kHz音頻範圍內,無抖動刺激時,量測到的值96dB,若在有抖動的情況下,量測到的是80dB。從這裡可以計算出,抖動產生的調變大於+10kHz及-12kHz,偏移是1.32ns rms或是12ps/(Hz。
更多精確的即時頻率量測,可以藉由正弦曲線的抖動刺激來產生,(圖三)解釋了這部分。被邊頻帶支配的錯誤信號,是71.4 dB低於12 kHz音調處。經過計算後,我們可以看出這符合3.5 ns的取樣抖動。這表示介於界面上的應用刺激抖動及在DAC上的取樣時脈,頻率在5 kHz以內,並沒有抖動衰減。(在抖動產生機制中,12kHz附近的裙帶有可能是低頻率的噪音)。
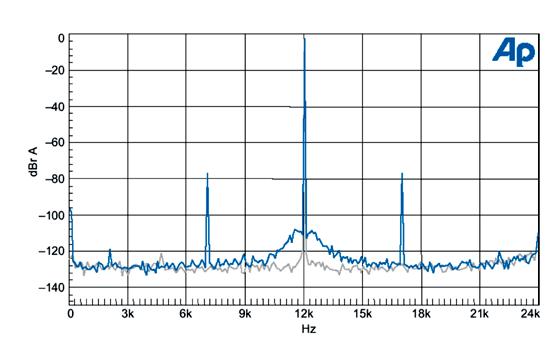
| 《圖三 DAC的FFT,灰色不含抖動,藍色含3.5ns rms 5KHz正弦波抖動》 |
|
由於在例子中的結果可能會有很大的變化,所以相同的測試會重複在不同的裝置。(圖四)顯示出FFT,值得注意的是5kHz邊頻帶比圖二衰減,而寬頻帶的抖動衰減與圖三有關。
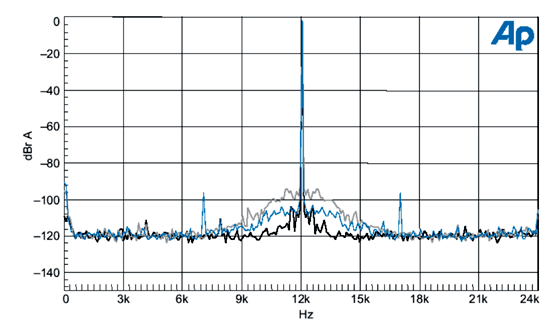
| 《圖四 灰色FFT:9.8ns峰對峰值的寬頻抖動;藍色:3.5ns rms 5KHz正弦波抖動;黑色:沒有抖動》 |
|
其它注意要點
從圖四中可以發現,寬頻帶的抖動在低頻率(靠近12kHz音調)時,是沒有衰減的,所以會有較大的振幅。當取樣抖動明顯增加時,和之前結果比較,不是因為抖動增加,而是時脈經由界面接收器及時脈回復系統,所產生的寬帶抖動。譬若說,取樣時脈恢復系統從接收器使用48kHz時脈,而且有個200kHz的頻寬抖動,抖動範圍中的24kHz到200kHz,是會被反射到從0Hz到24kHz的範圍內。因此這抖動噪音密度在24kHz範圍內增加10 log(200/24)=9.2dB。
另一個要注意的是低頻抖動,即使在沒有抖動刺激和正弦刺激低頻率抖動增加的情況下。這些影響不會反應在線性抖動轉移函數,但是表示了低頻率本質抖動。藉由在抖動產生機制內的低頻雜訊來增加5kHz音調抖動。
取樣抖動與資料抖動敏感性
J-test是AES3的測試信號,利用相同的時間提供一個基本高振幅的音調來刺激資料,得到最大的資料連慣性。這測試是用來刺激資料,得到最差程度的資料抖動。測試信號是由兩個元素所組成,第一個是在4個取樣的週期中,沒有加方波的高頻抖動(dither)。這週期我們使用十六位數符號表示。
C00000 (-0.5)
C00000 (-0.5)
400000 (+0.5)
400000 (+0.5)
當信號用取樣速率48kHz轉換到類比時,這信號將產生一個正弦波-3.01dB FS在12kHZ的振幅。(它看起來像是方形波,帶有-6.01dB FS的峰值振幅,但是在一個適當的限頻帶系統中,這順序的數值代表一個-3.01dB FS振幅的正弦波)。
進一步到第二個元素時,一個沒有高頻抖動(dither)的24位元方波形,振幅是1LSB,則會介於下列間做切換而成:
000000 (0)
FFFFFF (-1 LSB)
在低頻率重複性的方波,對於48kHz的取樣頻率而言,通常使用250Hz,這頻率並不精確,但是通常被拿來使用,就像是在AES3通道狀態資料塊中192取樣,形成信號同步一樣。
這些信號的合併結果如下列192取樣週期所形成的24位元資料數值。
C00000 C00000 400000 400000 (x24)
BFFFFF BFFFFF 3FFFFF 3FFFFF (x24)
這低頻率一致的交替在22LSBs數值,產生強的抖動頻譜元素在250Hz而且會有奇頻頻率產生。在(圖五)中,已經檢測出抖動信號,FFT已經圖解這情況(但是使用的是384週期J-test的版本產生一個125Hz的較低速率)。其內部符號干擾已經由電纜激發而感應。振幅軸線是以秒rms來表示,測試在工作在48kHz取樣頻率。元素在125Hz有個19.91ns的振幅,在界面信號上觀察到的抖動是大概在35ns峰對峰值:這抖動的圖解是波形的一部份,振幅有一部分是在這裡被降低。
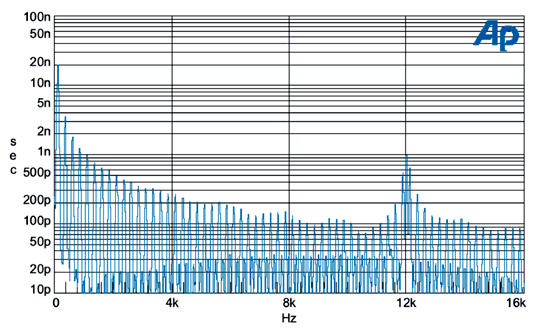
| 《圖五 經過cable模擬的J-test抖動頻譜》 |
|
(圖六)表示,測試裝置與應用J-test類比輸出的FFT,抖動邊頻帶確實順著界面抖動頻譜,代表這測試裝置是容易受到在界面上的數據抖動。
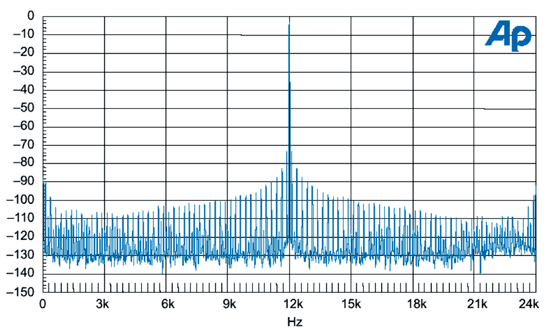
| 《圖六 經過cable模擬後,J-test所產生的抖動調變的FFT頻譜》 |
|
每個邊頻帶的形狀,與前面圖中的界面抖動頻譜相符合,所以我們也可以做個結論,在這頻帶內,它並沒有抖動濾波。125Hz的邊頻帶是每個大約是70dB,低於刺激音調(67dB是對於兩個一起的邊頻帶)。符合取樣抖動在振幅頻率,如(公式三)所示。

| 《公式三antilog((104-67)/20)/12=6ns rms》 |
|
清晰度的考量
清晰度可以用來確認及量測取樣抖動。但是如何分辨是否太多呢?由Eric Benjamin及Benjamin Gannon發表的論文中,描述實際研究發現最低抖動程度,抖動大概是在10ns rms時,會有一個顯注的差異,這是利用17kHz與高振幅測試正弦音調來作實驗。在音樂中,沒有任何這相關主題發現抖動低於20ns是可聽到的。
論文中發展出一個對於抖動可聽度的模型,以最差的音頻信號音調的信號,包含掩膜(masking)影響為基礎。包括:「掩膜理論建議最大的抖動,並不會一定產生可聽的影響,這是憑著抖動的頻譜而定。在低頻率,這程度是較大於100ns,與一個明確的近路在高於100Hz,到一個在500Hz較低的大約是1ns(峰值)的限度,在24kHz下降到大約是這頻率在6dB per octave到大概是10ps(峰值),對於系統來說,這音頻信號是120dB高於聽覺點。」
從更多最近研究觀點來看,這有可能被考慮得太過小心;無論如何,這考慮對於取樣抖動低於100Hz有可能是聽不到的,這原因是與抖動高於500Hz時做比較時,需多於40dB的因素,在決定像是有關於低及高頻率取樣抖動的重要性時,抖動高於500Hz時做比較是有幫助的。