|
|
| 無線通訊系統晶片之應用與技術架構(上) |
|
【作者: 張景祺,汪重光】 2003年09月05日 星期五
|
|
瀏覽人次:【17404】
近年來無線通訊蓬勃的發展,除了語音的傳輸外,高速的資料傳輸也隨著網路的發展更顯得重要性。無線通訊具有許多優點,如行動性、易於安裝及部署彈性等,但由於無線傳輸通道環境的限制,無線通訊品質的提升成為重要的課題。由於正交分頻多工(orthogonal frequency division multiplexing;OFDM)技術其特殊的調變方式在對抗通訊通道中多路徑衰減(multi-path fading)的環境時非常有效,同時其所使用的頻域等化器(frequency domain equalizer)在硬體的需求上非常少,因此,越來越多的無線通訊系統在新的標準誕生時都採用正交分頻多工做為其調變方式。
正交分頻多工調變技術在寬頻(broadband)傳輸的應用上有許多的優點,包括有:可根據傳輸通道的特性來動態的調整其傳輸率(data rate);對脈衝雜訊(impulse noise)有抑制能力;可彈性調整頻帶使用率(spectral efficiency),即可對干擾訊號產生無效的頻帶(spectral null)來加以抑制;面對無線通訊通道多路逕衰減時,可以有效的抑制訊號符元間干擾(inter symbol interference;ISI)等。但它的缺點就是對於載波頻率及相位偏移非常敏感,因此在設計系統架構時必須額外注意。正交分頻多工調變技術目前正廣泛應用在數位用戶迴路(digital subscriber loop;DSL)、數位聲音廣播系統及數位影像廣播系統(DAB、DVB)、無線區域網路(wireless LAN、IEEE802.11a/g)的標準及最後一哩無線傳輸系統(wireless MAN、IEEE802.16a/b)的標準等。
本文的內容首先會對正交分頻多工的技術做簡介,再來會探討其接收機同步的問題及通道的效應,接著會介紹傳收機系統架構的設計方法,包括基頻部份電路、類比前端電路及射頻電路架構選擇。
正交分頻多工(OFDM)技術概說
正交分頻多工是一種多載波調變(multi-carrier modulation;MCM)的技術,多載波調變的訊號是由數個窄頻(narrow band)等頻寬間隔的次載波(sub-carriers)調變訊號所組成,以達到最高的頻帶使用率。其技術是將一個單一的位元串流(bit stream)細分成數個位元串流Xn,k,如(圖一)所示,以此降低了每個串流的位元速率(bit rate)。每個位元串流再對映到相互正交的次載波上(k(t),然後以非常低的位元速率傳送出去以此避免符元間干擾。由於次載波間的正交特性,在接收端解調訊號時可避免於多重的次載波間發生資訊互擾(crosstalk)。
正交分頻多工調變系統是利用循環字首(cyclic prefix;CP)來免去接收機須對通道分散(channel dispersion)現象做延遲等化(delay equalization),同時也輔助接收機的同步(synchronization)機制。循環字首是將正交分頻多工符元(OFDM symbol)波形的末段部份複製並串接到符元的前端,其長度是約略大於通道的延遲延展(delay spread)。有了循環字首的安排則可抑制符元間干擾,此外由於符元前後是重覆的兩段波形,則可以被接收機利用做為同步調整的應用。
正交分頻多工的系統是利用逆向快速傅利葉(IFFT)來產生數位的訊號,一個逆向快速傅利葉的點數若為N則在頻域(frequency domain)上有N個次載波的符元且次載波相互間的頻域間隔為1/(N(t),其中取樣週期為(t,經過逆向快速傅利葉運算後會產生一個N(t的時域(time domain)波形。一個完整的正交分頻多工訊號符元含有N+L個取樣資料,如(圖二)所示,其中包含N個逆向快速傅利葉所產生的資料及L個循環字首。接著經過數位限頻濾波器(pulse shaping filter)後再由數位轉類比單元(digital to analog converter;DAC)合成為連續的類比訊號並透過射頻的電路經由天線發送出去。在接收端方面則是發送端的逆向訊號處理,數位訊號經快速傅利葉(FFT)解調後即可取得原先所傳送的位元串流。一個正交分頻多工完整的系統架構圖表示在(圖三)。
接收機同步的問題與通道效應
在一般通訊系統中有兩個同步的問題必須去處理:一是取樣同步(timing synchronization)、一是載波同步(carrier synchronization)。取樣同步的問題發生在發送機(transmitter;TX)與接收機(receiver;RX)之間的取樣頻率(frequency)與相位(phase)有誤差,換句話說就是發送機的數位轉類比單元與接收機的類比轉數位單元(analog to digital converter;ADC)之間的取樣頻率與相位有誤差,如(圖四)所示。若接收機的取樣回復(timing recovery)機制未能達到理想的取樣時基(jitter)要求,則會造成訊號的訊雜比(signal to noise ratio;SNR)下降,進而提高了位元錯誤率(bit error rate;BER)。
在同調(coherent)的通訊系統中,基頻(baseband)的訊號則會經過發送機的中頻(intermediate frequency;IF)單元或射頻(radio frequency;RF)單元做升頻(up convert)的動作,也就是經由載波(carrier)做頻率調變(modulation)後再傳送到通道之中;而在接收機方面則將接收到的通帶(passband)訊號由接收機的中頻單元或射頻單元做降頻(down convert)的動作,也就是經由載波做頻率解調(demodulation)後以取回基頻訊號再交由後端的基頻訊號處理單元做進一步的訊號處理。
在發送機與接收機兩端之間的升頻與降頻處理都必須各別仰賴一個局部振盪器(local oscillator;LO),因兩端起動(power on)時間不定會造成振盪器的相位誤差之外,由於溫度、雜訊或製程變異的影響會使得這兩端的局部振盪器有頻率的誤差,而這都會造成接收機收到的訊號在訊號星座(signal constellation)上旋轉,如(圖五)所示,使得訊號的訊雜比下降同時也提高了位元錯誤率。而在正交分頻多工的通訊系統中,接收機收到的時域訊號會經由快速傅利葉處理後轉變為頻域上的訊號,此時取樣同步與載波同步的問題將會對每個次載波造成不同的影響使得同步的問題更為複雜化。
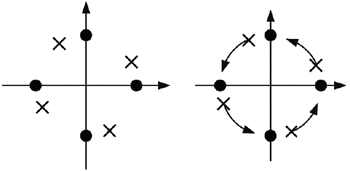
| 《圖五 載波相位誤差及頻率誤差時所接收到的訊號星座圖現象 ((:傳送,(:接收)》 |
|
此外正交分頻多工的通訊系統還必須額外做一個同步的回復機制:符元同步(symbol synchronization)。在發送機端將連續的位元串列分配給N個次載波後,以一整個資料區塊(block)一次同時做N點逆向快速傅利葉運算以產生N點的時域取樣資料,再加上L點的循環字首形成一個完整的正交分頻多工訊號符元,接著再經過平行轉序列(parallel to series;P/S)的處理,如圖二所示,如此不斷的重覆動作以形成無數個連續的基頻訊號如下:
@內文在式子中的Xn,k是第n個正交分頻多工符元上第k個次載波的符元,且以複數的形式表示;Tu是快速傅利葉的區段時間,Tg則是循環字首的區段時間Ts=Tu+Tg;fk=k/Tu,取樣週期T=Tu/N。
而在接收機前端則必須透過符元同步的機制以找出連續訊號波形中快速傅利葉區塊(FFT window)的起始點,再經過序列轉平行(series to parallel;S/P)的處理,接著將循環字首去除並透過N點快速傅利葉以一個區塊接一個區塊的運算來解調出原本所發送的位元串流。由此可知,一個正交分頻多工的通訊系統若應用在無線傳輸時則必須同時解決三個同步的問題;若是應用在基頻傳輸系統如數位使用者迴路,則可免去載波同步的機制。當同步的問題都被理想的達成時,則接收機收到的基頻訊號如下:
|
(公式四)為具多路徑衰減的無線通訊通道模型,而w(t)(時間函數)為可加性高斯白雜訊(AWGN)。在訊號傳輸過程中假設通道在一個正交分頻多工符元傳輸過程為靜態(static)或半靜態(quasi-static),則訊號在經快速傅利葉運算解回後第n個正交分頻多工符元中的第k個次載波訊號如下:
其中Hn,k為通道轉換公式(channel transfer function;CTF)在第n個正交分頻多工符元中的第k個次載波頻率位置的頻率響應(frequency response)。此即為通訊通道在頻域上對每一個次載波各別造成振幅及相位的影響,理想上可視為平坦(flat)的響應,而這也是多載波調變系統優於單一載波在面對通訊通道做等化(channel equalization)處理時硬體複雜度的地方。接下來就針對各種同步問題與通道效應對接收機在解調次載波時所造成的影響做更深入的探討,而同時會假設其他的影響不存在以簡化複雜度。
同步問題與通道效應對接收機之影響探討
符元同步(Symbol Synchronization)
接收機在做符元同步時若發生m個取樣點的誤差,接收機收到的基頻訊號如下:
其中必須達到mT<Tg,否則會造成次載波間的載波間干擾(inter carrier interference;ICI),而m為整數且T為取樣週期。訊號經快速傅利葉解回後第n個正交分頻多工符元中的第k個次載波訊號如下:
由此可知,訊號經快速傅利葉後所得的次載波將會造成訊號星座旋轉的現象,且旋轉的角度會依次載波編號由0度到2mπ(N-1)/N度呈線性遞增的誤差旋轉,如(圖六)所示為64點快速傅利葉的例子。
取樣同步(Timing Synchronization)
若接收機取樣有頻率及相位的誤差時,接收機收到的基頻訊號如下:
其中|l|<0.5,並且接收機以(1+()T為新的取樣週期。訊號經快速傅利葉解回後第n個正交分頻多工符元中的第k個次載波訊號如下:
首先,假設取樣頻率誤差為零((=0),亦即接收機只有取樣相位的誤差(|l|<0.5),則透過上式可以發現,除了載波間干擾為零之外,上式則可簡化如下:
由此可知,訊號經快速傅利葉後所得的次載波將會造成訊號星座旋轉的現象,且旋轉的角度會依次載波編號由0度到2lπ(N-1)/N度呈線性遞增的誤差旋轉,會類似圖六所示,唯誤差值最大值(k=N-1)會小於(,符合先前|l|<0.5的假設。另外當接收機取樣的初始相位誤差為零(l=0),且僅存在取樣頻率誤差時,則訊號經快速傅利葉解回後第n個正交分頻多工符元中的第k個次載波訊號如下:
由此可知,訊號經快速傅利葉後所得的次載波除了訊號星座旋轉的現象外,每個次載波的振幅也會受到改變,同時次載波間會有載波間干擾。然而,以目前的半導體電路設計技術而言,發送機與接收機之間的取樣誤差頻率相對於預定取樣頻率比值可限制在正負數十個百萬分之一(ppm)的範圍內,接收機因取樣頻率誤差造成訊號訊雜比衰竭量並不會太顯著,而真正影響訊號解調後的品質是取樣相位的誤差。不過,相位是來自頻率的積分,在設計接收機時不可忽視取樣頻率誤差的存在。
載波同步(Carrier Synchronization)
發送機與接收機之間的載波頻率及相位的誤差除了來自局部振盪器不同調外,無線傳輸通道的都普勒推移(Doppler shift)也會產生載波頻率的誤差量。若接收機載波有頻率及相位的誤差時,接收機收到的基頻訊號如下:
其中載波頻率誤差為(f而相位誤差為θ;(k=NT(f。訊號經快速傅利葉解回後第n個正交分頻多工符元中的第k個次載波訊號如下:
從(公式十三)可以發現,載波相位的誤差會對所有的次載波訊號星座造成相同角度(θ)的旋轉。而載波頻率的誤差除了對各別的次載波造成訊號星座不同的旋轉外,每個次載波的振幅也會受到改變,同時次載波間會有載波間干擾。雖然發送機與接收機之間的載波誤差頻率相對於預定載波頻率比值可限制在正負數十個百萬分之一(ppm)的範圍內,但由於預定載波頻率在無線傳輸系統的應用裡都為數個千兆赫(GHz),換言之,要以基頻的訊號處理單元來補償載波頻率的誤差時,微量的載波頻率誤差都會造成顯著的訊號訊雜比衰竭。
通道效應(Channel Effects)
不同於有線傳輸通道(wired channels)的特性,無線傳輸通道的特性是多變化且不可預測的,而且經統計歸納所得的通道模型是與當時傳輸環境有密切的關係。通道模型會根據其變動的行為程度來加以描述,可分為大程度變動(large-scale variations)及小程度變動(small-scale variations)。大程度變動包括訊號強度的路徑消退(path loss)及相對於路徑消退的變動或稱為模糊衰減(shadow fading),後者起因於大型障礙物;小程度變動是短距離或短期間傳遞時訊號強度的快速變動,起因於多路徑傳遞(multi-path propagation),且在寬頻傳輸系統時會造成頻域衰減通道(frequency-selective fading channel)。正交分頻多工的系統是將寬頻的訊號分成多個互相正交的窄頻來傳輸,因此接收機收到訊號時雖受到多路徑傳遞的影響造成頻域衰減通道,但在窄頻寬的次載波所面對的通道效應則可視為平坦效應,如(公式五)及(圖七)所示。
結語
在針對無線通訊系統的新興主流調變技術──正交分頻多工進行概略介紹,且對可能產生的同步問題與通道效應對接收機之影響進行深入探討後,下一期的文章中將繼續為讀者剖析傳收機架構的設計方法,包括基頻部份電路、類比前端電路及射頻電路架構之選擇。
(作者張景祺為臺大電機所博士班研究生,汪重光為台大系統晶片中心研究教授)
|