對於介於放大器與ADC之間的抗混疊濾波器設計而言，

系統性的做法將有助於設計人員處理涉及其中的各種因素、參數與設計取捨。

以主動式前端放大器驅動高速轉換器時，抗混疊濾波器的設計是相當困難的任務。對抗混疊濾波器的正確理解很重要，因為反鋸齒的特性能防止主要頻段以外不要的雜訊落入頻段內，所以瞭解好的抗混疊濾波器的必須性乃是完善高速類比訊號鏈設計的關鍵。在實作階段必須審慎考量各種細節因素。

中頻取樣與奈奎斯特(Nyquist)考量

中頻取樣 (IF ; intermediate frequency)允許設計者從訊號鏈省去一個混頻降頻(mix-down)級，又可提升性能，此其經由減少整體元件數量而降低了系統雜訊，從而維持良好訊號雜訊比(SNR)。某些特定條件之下，又能因此降低混頻器造成的本地振盪器訊號洩漏(local oscillator (LO) leakage )現象，達到增進無雜散動態範圍(SFDR)的效果。

基頻取樣適用於主要訊號或頻率落在第一奈奎斯特區域( first Nyquist zone)的狀況，但某些轉換器仍然可在高於第一奈奎斯特區取樣，這被稱之為欠取樣(undersampling )或中頻取樣 (IF sampling)。如圖1所示，其訊號落在第四奈奎斯特區，可看出此訊號影像或鋸齒被反射回第一奈奎斯特區上，就像是個20MHz訊號。

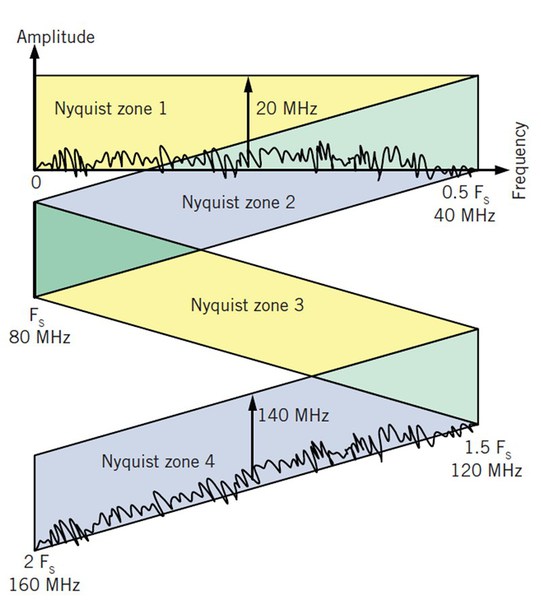
圖一 : 欠取樣(undersampling )或中頻取樣 (IF sampling) 適用轉換器在高於其兩倍取樣頻率(F_S)之奈奎斯特區進行取樣。舉例而言，若ADC取樣頻率為80 MHz 而量測頻率為140 MHz 則其訊號落在第四奈奎斯特區。

而大多數快速傅利葉轉換(FFT)分析器，例如Visual Analog，只會描出第一奈奎斯特區(0到0.5F_S)的傅利葉轉換。因此，假如主要頻率高於0.5F_S，則影像會被向下反射至第一奈奎斯特區(或稱為基頻) ，而這很可能會因為混附波(spurious tones)出現在主要頻段內而讓情況變得混亂。

根據Walt Kester在 High-Speed Design Seminar書中所述，類比數位轉換器(analog-to-digital converter ; ADC)可大於0.5F_S取樣率且不違背奈奎斯特準則：訊號必須以不少於自身頻寬兩倍的速率來進行取樣方能保有其完整內容。關鍵在於訊號頻寬的所在位置，只要訊號不重疊並保持在單一個奈奎斯特區之內即符合奈奎斯特準則，而唯一動到的是第一奈奎斯特區域至其上層的位置。

@大標:開始抗混疊濾波器的設計

設計開始

抗混疊濾波器有助於減少來自於不需要的奈奎斯特區訊號內容，避免頻帶內(in-band)鋸齒及破壞訊號鏈的動態效能。抗混疊濾波器的設計通常使用LC網路，加上明確定義的信號源與負載阻抗，以達到所需相關停止帶(stop-band)與通帶(passband)特性。濾波器網路實作上可沿用各式各樣的濾波器合成做法的參考書，其中常用柴氏(Chebyshev) 或巴氏(Butterworth)多項式來定義濾波器轉換函數。

濾波器轉換函數的格式完全取決於應用特性的需求，例如巴氏濾波器顯現大致渾圓響應，具有最佳通帶平坦度(0 dB 的漣波)與良好相位響應。反之，柴氏濾波器可達到較佳阻帶衰減或滾降(roll-off)，卻犧牲些通帶平坦度(漣波增大)。

有些以軟體為基礎的濾波器程式可以簡化這些問題，諸如Filter Free 4.0(Nuhertz Technologies) 、QUCS( Quite Universal Circuit Simulator)或ADS(Advanced Design System, Agilent Technologies)。初步可用放大器/ADC介面設計，假設其使用的帶通濾波器(bandpass filter)可在頻寬、訊號雜訊比(SNR)與無雜散動態範圍(SFDR)等指標達到最佳效能：

．放大器必須以其資料手冊所建議的正確dc負載運作以達最佳效能。

．放大器與濾波器所呈現的負載之間必須配置合適的串聯電阻以避免出現通帶內的異常峰值。

．使用外部並聯電阻可降低對ADC的輸入，並且在ADC與濾波器之間配置合適的串聯電阻，可降低通帶峰值。

類比前端電路的設計其實有點「牽一髮動全身」的味道，

舉例來說，調整電阻就會影響到SNR值的變化。

抗混疊濾波器設計運用在相對較高輸入阻抗的高速ADC與低阻抗驅動源(放大器)，若以一組廣義電路(圖二)進行理解，其核心設計過程具有以下七個步驟：

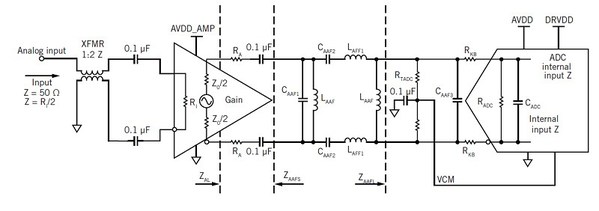
圖二 : 這種廣義電路類似多數高速差動放大器/ADC介面，用於解釋經由使用多數高速ADC的相對高輸入阻抗與相對低驅動源阻抗以最佳化濾波器全插入損耗。

．設定外部ADC終端電阻R_TADC 使並聯組合R_TADC 與R_ADC 其值介於200 Ω 與400 Ω之間。

．根據實驗或ADC資料手冊建議選擇R_KB ，其值一般介於5 Ω 與36 Ω之間。

．根據下式計算濾波器負載阻抗：Z_AAFL=2R_TADC | | (R_ADC+2R_KB )

．設定放大器外部串聯電阻R_A 。若放大器差動輸出阻抗介於100 Ω 與200 Ω之間則將R_A 設成低於10 Ω；若放大器差動輸出阻抗不高於12 Ω則將R_A 設成介於5 Ω 與36 Ω之間。

．根據下式設定Z_AAFL 使放大器全負載Z_AL 可被特定的差動放大器最佳化：

Z_AL=2R_A+Z_AAFL

．計算濾波器源極電阻：Z_AAFS=Z_O+2R_A

運用設計程式或表設計濾波器時，使用相同源阻抗值Z_AAFL 與負載阻抗值Z_AAFS ，此其有助於降低濾波器損耗，而任何兩端阻抗之差距會造成10*log(input Z/output Z)的損耗。例如輸入阻抗為50 Ω輸出為200 Ω時，濾波器損耗為-6.0 dB 或10*log(50/200)。並且增加 10%頻寬以確保頻率展開的平坦度。

經過上述初步計算階段，還必須根據下列規格快速檢閱電路細節：

．C_AAF3 之值應至少為10 pF使其大於C_ADC 值數倍，如此可最佳化濾波器對於C_ADC 變動的敏感度。

．Z_AAFL 與 Z_AAFS 比值不可高於7，使濾波器不超過多數設計程式的限度，理想上這兩個值應該設相等以最佳化損耗。

．C_AAF1 之值至少為5 pF以最佳化濾波器對於寄生電容與其他元件值變動的敏感度。

．L_AAF 電感之合理設定值約在數個nH。

．C_AFF2 與L_AAF1 值應合理設定，必須留意有時電路模擬器會把這兩個值設成過高或過低。通常將其與較佳標準元件值保持一定比率以維持相同共振頻率(如圖3)。

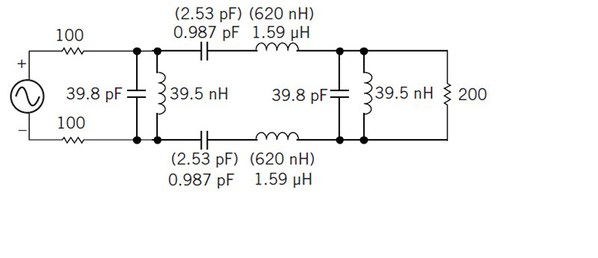
圖三 : 若C_AFF2 與L_AAF1不為合理設定，則使用標準L與C值並保持一定比率以維持相同共振頻率。

有些狀況下濾波器設計程式會跑出多種解，特別是那些高階濾波器，而採取最合理元件組合值的解法應是其中最適宜可行的，並且還得選擇相符於並聯電容器末端的組態。使其能與ADC的輸入電容結合。

設計取捨

介面電路的參數彼此之間有高度互動性，因此絕難針對特定規格指標(如頻寬、頻寬平坦度、訊號雜訊比與無雜散動態範圍、與增益)加以最佳化。然而頻寬響應常發生的峰值現象可經由調整R_A 與R_KB 值加以最小化，

圖四指出通帶峰值高低與輸出串聯電阻值R_A升降之間關係。但隨著電阻升高造成更嚴重的訊號衰減，放大器須驅動較大訊號以填滿ADC的滿量程輸入範圍。

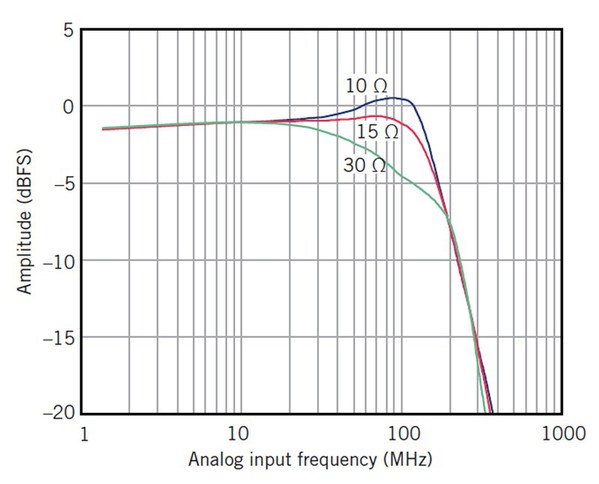
圖四 : 增加輸出串聯電阻R_A可降低通帶峰值，然而卻同時造成訊號衰減，放大器須驅動較大訊號以填滿ADC的全部輸入滿量程。

調整R_A也會影響訊號雜訊比(SNR)，調高R_A 值而降低頻寬峰值，因減少頻寬內不要的雜訊可能會些微增加SNR。

設定ADC的輸入端串聯電阻R_KB 可最佳化ADC內部取樣電容剩餘電荷注入所造成的失真現象 。調高R_KB也會降低頻寬峰值，卻也會造成訊號衰減效應，放大器須驅動較大訊號。

對於通帶中心頻率的最佳化可經由微調C_AFF2串聯電容達成，由此設計者可安排應用所需的最佳頻率覆蓋。

一般來說，終端電阻R_TADC 的設定必須維持ADC淨輸入阻抗在200 Ω至400 Ω之間，與多數典型放大器負載相符，太高或太低都會影響到放大器的線性度。

設計整合

經由這些步驟來到窄通帶接收器前端設計，基於ADI的超低雜訊差動放大器驅動器與ADC (14位元，取樣率250-Msample/s) (圖五)。

三階巴氏抗混疊濾波器以效能與介面需求進行最佳化。濾波器網路與其他元件全插入損耗僅5.8 dB。此ac耦合設計採用0.1 μF電容以阻擋放大器、終端電阻與ADC之間的共模電壓。

整個電路具有18 MHz頻寬與3dB通帶平坦度，訊號雜訊比(SNR)與無雜散動態範圍(SFDR)分別是71.7 dBFS與92 dBc(以127 MHz輸入之下)。取樣頻率為205 Msamples/s，中頻訊號所在的第二奈奎斯特區域介於102.5 MHz 與205 MHz之間。

其電路以寬廣的頻寬(3 GHz)1:2變壓器接收單端輸入並轉為差動訊號。ADI的差動放大器(6 GHz) 在12 dB訊號增益運作之下具有100 Ω輸入阻抗，以補償濾波器網路與變壓器的插入損耗(約5.8 dB)，整體提供5.5 dB訊號增益。

輸入訊號具有+1.5 dBm可在ADC輸入端產生滿量程1.75 V p-p差動訊號。根據標準設計程序採用的抗混疊濾波器為三階巴氏濾波器，乃是由於其通帶平坦特質，而三階濾波器可獲致1.05的ac雜訊頻寬比。為了達到最佳效能，以淨差動負載 200 Ω載入差動放大器， 所串聯的15 Ω電阻區隔濾波器電容與放大器輸出。 以100Ω 電阻並聯下游阻抗，再加入30 Ω串聯電阻獲致 217 Ω淨負載阻抗。

ADC輸入端串聯的5 Ω電阻隔離濾波器與放大器內部開關暫態，2.85 kΩ輸入阻抗乃是由ADI的ADC(14位元，取樣率250-Msample/s)資料手冊所定。可單純採用並聯追蹤模式(parallel track mode)值定出中頻中心。

三階巴氏濾波器設計以差動式200 Ω訊號源阻抗與200 Ω負載阻抗最佳化濾波器損耗，具有中心頻率127 MHz、3 dB通帶平坦度與20 MHz頻寬。圖三顯示經由標準濾波器設計程式所計算的結果。以較高串聯電感前提之下，1.59 μH電感減低至620 nH，而0.987 pF電容隨之增為2.53 pF，維持相同的127 MHz共振頻率，並且具備更切實際的元件值。

以電容器置於ADC附近以減低或吸收輸出入相互干擾電荷，其電容為37.3 pF，由第二並聯電容值減去ADC內部2.5 pF電容而得。

圖五顯示實作調整寄生迴路後濾波器被動元件設定值。其總結所測系統效能為：18 MHz頻寬(中心頻率127 MHz)與3 dB通帶平坦度，網路全插入損耗為5.8 dB。圖六顯示頻率響應與SNR/SFDR對應圖 。

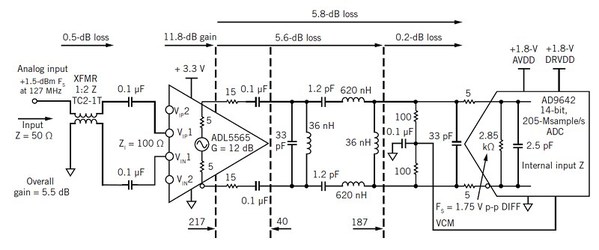
圖五 : 文中所述過程獲致基於三階巴氏抗混疊濾波器的窄通帶接收器前端設計，其中 0.1-μF電容用以阻擋放大器、終端電阻與ADC之間的共模電壓。

圖六-上

圖六-下

以曲線圖顯示不同頻率之下的通帶平坦度效能(上圖)與SNR/SFDR效能(下圖)，二者取樣率皆為205 Msamples/s。

結論

對介於放大器與ADC之間的抗混疊濾波器設計而言，不同因素、不同參數取捨設定的困難程度甚高。在先前設計之中，所有參數皆被賦予相同的權重，而從參數的取值上就直接反映在系統整體介面效能上。而有些設計則會針對系統應用所需，從SFDR、SNR或輸入驅動等級各方面考量來進行特定參數最佳化。

（本文作者現任ADI 軍事航太應用工業與儀器部門資深應用工程師，曾在轉換器介面、轉換器測試與類比訊號鏈等相關應用領域發表諸多論文。）